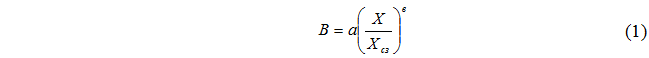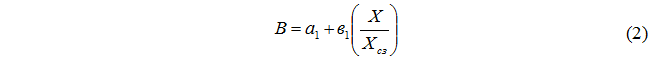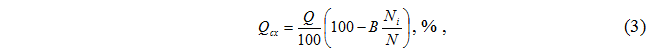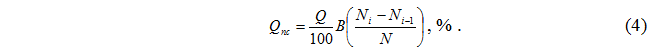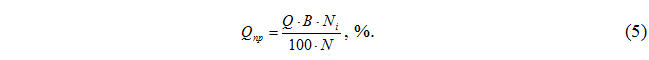Calculation of material balances during the processing of husked wheat grain in reduced grinding structures

Calculation of material balances during the processing of husked wheat grain in reduced grinding structures

O.P. Vereshchynskyi, Ph.D. technical Sci.,

E.I. Kharchenko, candidate technical Science.

National University of Food Technologies

The development of mathematical modeling of wheat grain grinding operations in multi-grade bakery mills is considered. The peculiarities of mathematical models for describing the quantitative indicators of the grinding balance have been determined. Quantitative indicators of the products of grinding husked wheat grain on the 1st shredding system are given, taking into account the values ​​of its husking index. The practical use of approximate engineering calculations of material flows in shortened structures for grinding hulled grain has been verified and recognized as possible. Graphical data are offered to clarify approximate calculations.

     Key words: grinding, mode, yield of coarse products, balance, grain peeling, granulometric composition.
The task of creating effective grain processing technologies cannot be solved without using the basic laws of technological processes, operations, sub-stages and stages presented in the form of models characterizing the change in quantitative and qualitative indicators of products during processing. Taking into account the multifactorial nature of technological processes, complex branched structures of flour production and the lack of stability of grain quality indicators, it is advisable to use deterministic models obtained both theoretically and as a result of statistical processing of experimental data, as a result of physical modeling. The goal of mathematical modeling of technological processes is to predict the quantitative and qualitative characteristics of material flows that occur during processing. Such models are, by their very nature, material balance equations. At the same time, the development of the material flow balance is the basis of the design of flour production technologies.
Until recently, the tasks of creating flour production technologies were based exclusively on the method of physical modeling. Therefore, the indicators of material balances obtained at pilot plants during a considerable period of research, carried out by a number of scientific teams and practitioners, formed the basis of typical projects. However, the reduction of milling structures by intensification of a number of processes using grain peeling is a relatively new direction of increasing the efficiency of flour production, therefore, the determination of indicators of their material flows goes beyond the existing typical solutions, which is obvious.
The most significant in the modeling of technological processes of flour production are the works of V.V. Vashkevicha, O.V. Gornetsa, V.A. Panfilov [1-3], which were summarized and developed by the work of G.N. Pankratova [4].
The basis of the development of G.N. The pankratov model of the grinding stage of flour production is the definition of patterns of size distribution of grinding products. The author conducted experimental studies of the dispersed composition of grinding products by constructing integral curves in the B – X/X_NW coordinate system. It was established that the obtained results can be approximated with high accuracy by a power dependence of the form:

where, B is the product of the product, %; X/X_sz is the relative size of the product, defined as the ratio of its true size X to the weighted average size of the particles of the mixture < em>X_sz.

   With somewhat less accuracy, the obtained results are described by a linear dependence of the form:

At the same time, the nature of the distribution of particles does not depend on the method of measuring their sizes, grinding system, modes, etc.
According to its content, the coefficient “a₁” characterizes the value of the product at X/X_sz  = 0. The coefficient “in₁” is the rate of change of the product with an increase in the size of the sieve holes. According to the hypothesis of A.H.M. Andreasen, with an “ideal” grinding process, the coefficients “a₁” and “v₁” should acquire values, respectively 0 and 0.5 (50%). It has been established that for most systems of developed grinding structures under their normative operating modes [5] the values ​​of the specified coefficients are really close to the specified ones. For a power-law dependence, the “ideal” process is characterized by the values ​​of a = 0.5, v = 0, which is essentially the same.
At the same time, it was established that in real grinding processes, the coefficients of the obtained power and linear equations significantly depend on the fractional composition of the initial mixture, kinematic and geometric characteristics of the rollers, grinding modes, etc. In addition, in the practice of grinding to evaluate the grinding mode, it is customary to use the yield indicator on sieves with certain hole sizes, which requires an assessment of the dimensions in the true dimension. The weighted average particle size X_cz, which is a component of the obtained formulas, also characterizes the grinding mode, but its value in most cases is unknown. Therefore, although the given formulas probably describe the law of distribution by size of grinding products, their application for practical calculations of material flows is not possible.On the basis of an experimental study of the above dependences for calculations of the theoretical balance of graded bakery grinding of wheat, G.N. Pankratov proposed graphs of the dispersed composition of grinding products. Such graphs are presented as a dependence of the product on the size of the sieve holes for a number of systems, grinding modes and grain quality that are standardized [5]. Thus, the obtained graphs have a limited application, which is determined by the normalized conditions. The balance of material flows at low grinding modes of hulled grain and intermediate products obtained from it, the feasibility of which is justified by the results of research [6, 7], cannot be reliably determined on the basis of the proposed graphs.
However, for engineering calculations of the theoretical balance, simplified formulas were proposed [4] for calculating a number of values ​​necessary for design practice.
The amount of step product Q_x from the ith sieve:

where, Q is the amount of product received on this system, %;

     B – the value of the given product, %;

     N_i – the linear size of the holes of the ith sieve, μm;

     N is the linear size of the sieve holes, which determines the value of the product B, μm.
The amount of intermediate product Q_pc obtained by passing a sieve with linear hole sizes N_i and exiting the sieve with the linear sizes of holes N_i-1:

The amount of passing product Q_pr from the ith sieve:

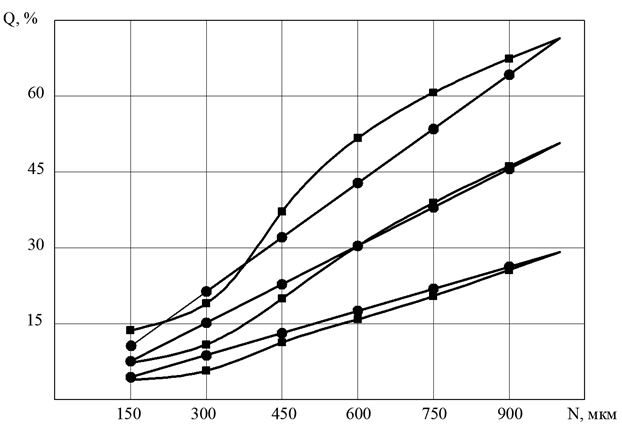
In comparison with the recommended regimes [5], the essential difference between the conditions predicted by the reduced structures is the grinding of grain with changed physical, mechanical and structural properties (husked grain) with the provision of high product yield values, which is most evident in the shredding process and especially on the first shredding system. In view of the above, we checked the possibility of approximate application of formulas 3, 4 and 5 for the specified conditions. Such a check was performed for grinding on the I shredding system hulled and unhulled grain with different values ​​of the total product. In Figure 1, graphs of the dependence of the yield on the sizes of the sieve openings, obtained experimentally (table 1) for non-hulled grain and grain with different indices of hulling, are shown by lines in the form of curves. Since the curves obtained with the same total yields and different indices of grain peeling turned out to be relatively close, the specified graphs were constructed based on average indicators. From the above, it can be seen that within the total product yield of 30…70% with increasing values ​​of the total product, the power-law dependence of the fractional distribution of the mixture particles is more pronounced. This is due to the fact that with an increase in the total product, the weighted average particle size decreases and in the range of sizes corresponding to the sizes of intermediate products, the value of Х/Х_сз< /em> exceeds 1.2…1.5, where according to formula 1, deviation from linearity is significantly manifested. In fig. 1, graphs of dependence calculated by formulas 3, 4 and 5 are marked with straight lines.The value of the total product of intermediate products was used as indicators of B and N, that is, the product at N = 1000 μm, which, as a rule, is always a known quantity in practical calculations. As can be seen from the above, the dependencies calculated by formulas 3, 4 and 5 roughly correspond to the experimental data.
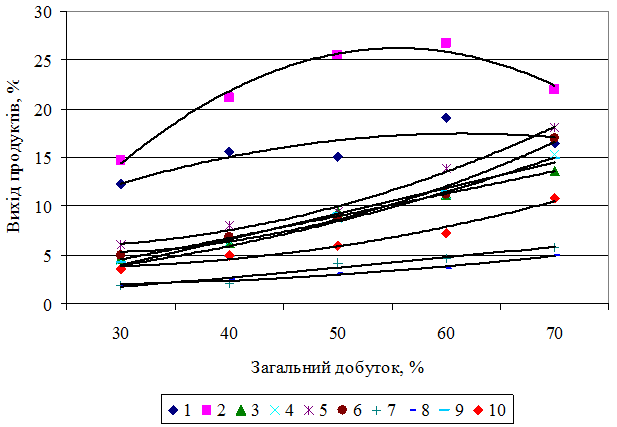
Further mathematical processing showed that it is difficult to determine a multifactorial relationship that would more accurately correspond to the results of physical modeling for the array of experimental data obtained, since there are no clear relationships between the nature of the distribution of intermediate products and the factors under investigation (total yield, peeling index and yield of intermediate products ). However, the obtained data in the form shown in fig. 2, if necessary, can be used to clarify the calculations of material balances made according to formulas (3), (4) and (5).

Fig. 1. Dependence of the amount of grinding product obtained on the first shredding system of husked wheat grain Q on the linear dimensions of the sieve holes N: ■ –  experimental data; ● – data calculated according to formulas (3), (4) and (5).
Table 1

Quantitative and qualitative indicators of grain grinding products on the 1st shredding system (quantity, % / ash content, %)

Fig. 2. Dependence of the yield of intermediate products and flour on the total product on the I broken system:
1.2 – the output of coarse grain during grinding, respectively, of unhusked grain and hulled grain (hulling index 8%);
3.4 – yield of medium grain when grinding, respectively, unhusked grain and hulled grain (hulling index 8%);
5.6 – output of fine grain during grinding, respectively, of unhusked grain and hulled grain (hulling index 8%);
7.8 – output of dunts during grinding, respectively, of unhusked grain and hulled grain (hulling index 8%);
9,10 – flour yield when grinding, respectively, unhusked grain and hulled grain (hulling index 8%).
Taking into account the fact that when choosing technological equipment of the grinding stage, the permissible error of its load can be 10…25%, and when calculating pneumatic transport – 10…30% per system, formulas 3, 4 and 5 can be used for approximate calculations of material flows obtained at grinding husked grain with low modes. If necessary, the obtained calculation data can be refined on the basis of the presented studies.
Literature:
1. V.V. Vashkevich Scientific and practical foundations of wheat milling technology (grinding department) [Text]: dissertation. … Dr. technical Sciences: 05.18.02 / V.V. Vashkevich – Barnaul.: MGAPP, 1995. – 366c.
2. Gornets O.B. Development of a model of the broken process of metal mills for the production of graded flour [Text]: diss. … candidate technical Sciences: 05.18.02 / O.B. potter – Barnaul.: Alt. GTU named after I.I. Polzunova, 1994. – 187c.
3. Panfilov V.A. Technological lines of food production. (theory of technological flow) [Text] / V.A. Panfilov. – M.: Kolos, 1993. – 288c.
4. Pankratov G.N. Scientific basis of perfection of flour milling production technologies [Text]: diss. … Ph.D. : 05.18.01 / G.N. Pankratov. – M.: MGUPP, 2001. – 364c.
5. Kroshko G.D. Rules for the organization and management of the technological process at flour mills [Text] / G.D. Kroshko [etc.]. – K.: Vipol, 1998. – 145c.
6. Dmytruk E.A. Abbreviated technological process of flour production [Text] / E.A. Dmytruk, V.B. Ilchuk, O.P. Vereshchynskyi, O.A. Chornyi, E.I. Kharchenko // Grain storage and processing. – 2009. – No. 2. – P.53-54.
7. Vereshchinsky A.P. Laws of grinding husked wheat grain [Text] / A.P. Vereshchinsky // Bread products. – 2012. – No. 12. – P.38-39.

A.P. Vereshchynskyi, E.I. Kharchenko

Calculation of material balances during processing

hulled wheat grain into flour

The development of mathematical modeling of wheat grain grinding processes during graded grinding is considered. The features of the mathematical models for the description of grinding balances are established. Quantitative and qualitative indicators of the products of wheat grain milling on the I-shred system, taking into account the indices of wheat husking before milling, are presented.  

Key words: grinding, mode, output of coarse products, balance, grain dehulling, granulometric composition.

 

A. Vereshchynsky, E. Kharchenko